수치 해석적 미분
테일러 전개
테일러 전개를 이용하여 함수 f(x)의 x에 대한 미분을 수치해석적으로 계산하는 공식을 유도할수 있다.
[테일러 전개의 소개]
http://en.wikipedia.org/wiki/Taylor_series
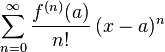
테일러 전개 공식
참고)미분이란 물리량1에 대한 물리량2에 대한 변화율이다.
해석적 방법으로 문제를 풀수 있지만 복잡한 미분 방정식일 경우 수치적 방법으로도 문제를 풀 수 있다.
수치적 방법으로 풀 수 있다는 것은 컴퓨터를 이용해서 문제를 풀수 있다는 것이다.
참고) 수치해석은 해석학 문제에서 수치적인 근사값을 구하는 알고리즘을 연구하는 학문이다.
다음은 수치해석적 방법으로 미분 문제를 푼 예이다.
테일러 전개를 이용해 f(x)함수를 a근처에서 전개했을 경우
함수 f(x)를 x=x제로 주위에서 테일러 전개하면, 미소 변위 h에 대하여 공식을 유도할 수 있다.
이렇게 산출된 공식으로 프로그램밍 로직을 구현하면 된다.
(h값이 작을수록 어떤 값에 대하여 빠르게 수렴하게 된다.)
MAX_STEP = 미소변위(h) => dx 의 값
f(x) = 미분할 함수(x*x)
2점공식 소스-c언어
#include <stdio.h>
#include <stdlib.h>
/* 1차 미분 계산 */
#define MAX_STEP 1000
#define dx (1.0/(float)MAX_STEP)
#define f(x) ((x)*(x)) //미분할 함수 x pow(2)
int main()
{
printf("Hello world!\n");
/* 구간 [0, 1] 에서 함수 f(x) = x^2의 미분을 MAX_STEP 개수 만큼의 */
/* 그물코 위치(meth points)에서 계산한다. */
FILE *fpt; /* 결과를 출력하비다. */
int i;
float x[MAX_STEP]; //x 좌표
float fx[MAX_STEP]; //y 좌표
float dfx[MAX_STEP]; //df() /dfx
fpt = fopen("diff_2point.txt","w");
for(i=0; i<MAX_STEP; i++){
x[i]=dx*i;
fx[i] = f(x[i]);
}
for(i=0; i<MAX_STEP-1; i++){
dfx[i] = (fx[i+1]-fx[i]) /dx;
fprintf(fpt, "%f %f %f \n", x[i], fx[i], dfx[i]);
printf("%f %f %f \n", x[i], fx[i], dfx[i]);
}
fclose(fpt);
return 0;
}
2점공식 결과 그래프
빨간색 선으로 된 그래프는 미분된 값들이다.
검정색 선으로 된 그래프는 미분되기 전에 대한 y값에 그래프이다.
3점 공식 소스-c언어
3점 공식 결과 그래프
2점공식과 3점 공식의 그래프의 비교
많은 점을 참조할수록 수치적 방법에 대한 오차 범위를 줄일수 있다.
수치적 방법에는 컴퓨터계산에 따르는 오차가 존재한다. 그 오차들을 많은 점을 참조할수록 오차를 많이 줄일 수 있다.
뉴튼-랩슨(Newton-Rahpson) 법
생활코딩 페이스북에서 김태균님이 흥미로운 주제대 대하여 언급하여 뉴턴법에 대하여 알아보았다.
http://www.facebook.com/groups/codingeverybody/permalink/550830794957461/
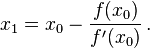
자바 언어를 이용하여 루트2(뉴튼법 이용)의 값을 구한 예제.
class Newton {
static double Function1(double x) {
return (x*x-2);
}
static double Function2(double y) {
return (2*y);
}
public static void main(String argv[]) {
System.out.println("Newton method");
double tolerance = 0.000000001;
double x = 2;
while( (Function1(x)/Function2(x) ) > tolerance )
{
x = x - (Function1(x) / Function2(x));
System.out.println("in loop " + x);
}
System.out.println("result : "+ x);
}
}
뉴턴법을 이용한 방의 넓이를 구하는 예
class Newton {
static double Function1(double x) {
return ((x*x) - 612);
}
static double Function2(double x) {
return ( 2*x);
}
public static void main(String argv[]) {
System.out.println("Newton method");
double i = 0;
double x = 10;
while( i < 100)
{
x = x - (Function1(x) / Function2(x));
System.out.println("in loop " + x);
i++;
}
System.out.println("result : "+ x);
}
}
C:\Users\developer\Documents\GitH
Newton method
in loop 35.6
in loop 26.395505617977527
in loop 24.790635492455475
in loop 24.738688294075324
in loop 24.738633753766084
result : 24.738633753766084
참조
위 소스는 링크의 글을 참조하여 작성하였습니다.
http://www.hanb.co.kr/network/view.html?bi_id=614
자바언어 수학 라이브러리 :


