Fast alle Zahlen, die in der Schulmathematik auftreten, sind die reellen Zahlen. Die Menge aller reellen Zahlen wird mit R bezeichnet.
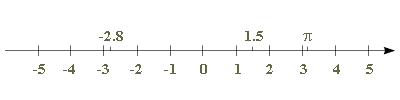
Reelle Zahlen stellen sich nun als Abstand vom Nullpunkt (0) dar. Punkte rechts von 0 werden als positive Zahlen und Punkte links 0 als negative Zahlen interpretiert.
Teilmengen von R
- Die natürlichen Zahlen (N): Es sind jene positiven reellen Zahlen, deren Dezimaldarstellung nach dem Komma abbricht (d.h. nach dem Komma nur Nullen enthält z.B. 5 dasselbe wie 5.0000).
- Manchmal will man mit 0 zu zählen beginnen. Wenn die Zahl 0 zu den natürlichen Zahlen hinzugeben wird, heißt die Menge N0 = {0} ∪ N = {0, 1, 2, 3, 4, ...}.
- Die ganzen Zahlen (Z): Es sind jene reellen Zahlen, deren Dezimaldarstellung nach dem Komma abbricht.
- Die rationalen Zahlen (Q): Es sind jene reellen Zahlen, deren Dezimaldarstellung von einer bestimmten Stelle an nur Nullen aufweist (z.B. 0.4) oder periodisch (z.B. -11.2181818) ist.
- Die rationalen Zahlen sind manchmal auch als Bruchzahlen bezeichnet werden, weil sie sich als Division einer ganzen Zahl durch eine ganze Zahl (d.h. ganze Zahl / ganze Zahl) darstellen lassen (z.B. 2/5 und 0.4, abgesehen von der unterschiedlichen Darstellungsweise, bestehen keinen Unterschied.
- Die irrationalen Zahlen (R - Q): Es sind jene reellen Zahlen,
- die nicht rational sind und
- deren Dezimaldarstellung weder abbricht noch periodisch ist
어휘: abgesehen von (except for ~를 제외하고), Bruchzahlen (분수), weder .. noch (부사임) .. (neither .. nor ...), Abstand (거리), jene (어떤~ 정관사변화), aufweisen (보여지다), periodisch (일정 패턴이 반복되는 영어의 periodically 와 똑같은 의미), abbrechen (어느 지점에서 멈춰지는, discontinued)


